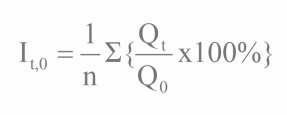Newest Post
Archive for April 2019
Angka Indeks
Angka Indeks adalah suatu angka yang dibuat sedemikian rupa sehingga dapat
dipergunakan untuk melakukan perbandingan antara kegiatan yang sama (produksi ekspor,
hasil penjualan, jumlah uang beredar, dsb) dalam dua waktu yang berbeda. Di
dalam membuat angka indeks diperlukan dua macam waktu yaitu:
1.Waktu dasar (Base period) yaitu waktu di mana suatu kegiatan (kejadian) dipergunakan untuk dasar perbandingan.
2.Waktu yang bersangkutan/sedang berjalan (Current period) yaitu waktu dimana suatu kegiatan akan diperbandingkan terhadap kegiatan pada waktu dasar.
Pemilihan Tahun Dasar.
Beberapa syarat yang perlu diperhatikan
dalam menentukan atau memilih waktu dasar adalah
1. Waktu sebaiknya menunjukkan keadaan perekonomian yang stabil, di mana harga tidak
berubah dengan cepat sekali.
1. Waktu sebaiknya menunjukkan keadaan perekonomian yang stabil, di mana harga tidak
berubah dengan cepat sekali.
2. Waktu sebaiknya usahakan paling lama
10 tahun atau lebih baik kurang dari 5 tahun.
3. Waktu di mana terjadi peristiwa
penting.
4. Waktu di mana tersedia data untuk keperluan pertimbangan, hal ini tergantung pada tersedianya biaya untuk penelitian ( pengumpulan data).
4. Waktu di mana tersedia data untuk keperluan pertimbangan, hal ini tergantung pada tersedianya biaya untuk penelitian ( pengumpulan data).
Indeks Tidak Tertimbang
1. Indeks harga relatif sederhana adalah indeks yang terdiri dari satu macam barang saja baik untuk indeks produksi maupun indeks harga misalnya indeks produksi ikan, indeks harga beras dll.
2. Indeks Agregatif adalah indeks yang terdiri dari beberapa barang (kelompok barang) misalnya indeks harga 9 bahan pokok.
1. Indeks harga relatif sederhana adalah indeks yang terdiri dari satu macam barang saja baik untuk indeks produksi maupun indeks harga misalnya indeks produksi ikan, indeks harga beras dll.
2. Indeks Agregatif adalah indeks yang terdiri dari beberapa barang (kelompok barang) misalnya indeks harga 9 bahan pokok.
Angka Indeks Sederhana Relatif Harga
Angka Indeks Sederhana Relatif Kuantitas
Angka Indeks Sederhana Harga Agregatif
Angka Indeks Sederhana Kuantitas Agregatif
Angka Indeks Sederhana Harga Rata-rata
Relatif
Angka Indeks Sederhana Kuantitas Rata-rata Relatif
Keterangan :
It,0 = Angka indeks tahun ke-t dibandingkan dengan tahun dasar
Pt = Harga masing-masing produk pada tahun ke-t
P0 = Harga masing-masing produk pada tahun dasar
Qt = Kuantitas masing-masing produk pada tahun ke-t
Q0 = Kuantitas masing-masing produk pada tahun dasar
n = Banyaknya produk yang diobservasi
It,0 = Angka indeks tahun ke-t dibandingkan dengan tahun dasar
Pt = Harga masing-masing produk pada tahun ke-t
P0 = Harga masing-masing produk pada tahun dasar
Qt = Kuantitas masing-masing produk pada tahun ke-t
Q0 = Kuantitas masing-masing produk pada tahun dasar
n = Banyaknya produk yang diobservasi
Contoh Soal:
Terima Kasih, Semoga Bermanfaat :)
Kemiringan Distribusi Data
Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data.
Kemiringan distribusi data terdapat 3 jenis, yaitu :
o Simetris : menunjukkan letak nilai rata-rata hitung, median, dan modus berhimpit (berkisar
disatu titik)
o Miring ke kanan : mempunyai nilai modus paling kecil dan rata-rata hitung paling
besar
o Miring ke kiri : mempunyai nilai modus paling besar dan rata-rata hitung paling kecil
Rumus untuk menghitung derajat
kemiringan distribusi data ( a3 )
a. Rumus Pearson
a. Rumus Pearson
b. Rumus Momen
- Data tidak berkelompok
c. Rumus Bowley
Rumus ini menggunakan nilai kuartil :
Rumus ini menggunakan nilai kuartil :
3 = Derajat kemiringan
X
i = Nilai data ke – i
= Nilai rata-rata hitung
f
i = Frekuensi kelas ke - i
m
i = Nilai titik tengah kelas ke – I
S = Simpangan baku
n = Banyaknya data
Jika a
3 = 0 distribusi data simetrisa
3 < 0 distribusi data miring ke kiria
3 > 0 distribusi data miring ke kanan
Keruncingan Distribusi Data
Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Keruncingan distribusi data ini disebut juga kurtosis. Ada tiga jenis derajat keruncingan, yaitu :
Leptokurtis : distribusi data yang puncaknya relatif tinggi
Mesokurtis : distribusi data yang puncaknya normal
Platikurtis : distribusi data yang puncaknya terlalu
rendah dan terlalu mendatar
Menentukan Ukuran Statistik
Deskriptif
Menggunakan Excel
Langkah-langkahnya:
1. Ketik data pada kolom A seperti contoh di atas
2. Pilih menu Tools pada menu utama
3. Pilih Data Analysis
4. Pilih Deskriptive Statistics pada daftar Analysis Tools
lalu klik OK
Ketika Box Dialog muncul:
Ø Ketik A2…A21 pada kotak Input Range
Ø Ketik C1 pada kotak Output Range dan pilih Summary
Statistics dan klik OK
Menggunakan Excel
Langkah-langkahnya:
1. Ketik data pada kolom A seperti contoh di atas
2. Pilih menu Tools pada menu utama
3. Pilih Data Analysis
4. Pilih Deskriptive Statistics pada daftar Analysis Tools
lalu klik OK
Ketika Box Dialog muncul:
Ø Ketik A2…A21 pada kotak Input Range
Ø Ketik C1 pada kotak Output Range dan pilih Summary
Statistics dan klik OK
Selesai, Semoga Bermanfaat :)
